Nicolás nos pregunta:
Buenas. Os escribo porque desde hace unos días me ha surgido una duda matemática importante. He pensado que, en un triangulo, dada la longitud de los lados se debería poder hallar el área, ya que solo hay un triangulo posible con esos lados; pero en cambio la única formula que conozco para el área del triangulo es la de base·altura/2.
Dos preguntas:
1 – ¿Cómo se calcula el área del triangulo a partir de los lados?
2 – ¿Por qué es tan poco conocido ese método, si aparentemente es el más útil en la vida real?
Espero que sepáis responder. Gracias.
Hay respuestas para tus dos preguntas, Nicolás.
La fórmula para calcular el área de un triángulo a partir de sus lados se conoce como Fórmula de Herón, en honor a Herón de Alejandría, un ingeniero griego que la demostró en su libro La métrica. La fórmula tiene esta pinta (S es el área o superficie y a, b y c los lados del triángulo):
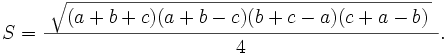
Y nada más verla comprenderás por qué no es la más usada. En cuanto te acostumbras, es más fácil usar un seno o un coseno para sacar la altura y usar la fórmula habitual que andar haciendo todas las cuentas de Herón.
¿El área de un triangulo? Sea como sea, es mejor no tratar con triángulos sino con rectángulos (2 triángulos iguales forman un rectángulo) y luego dividir entre 2. ¿no?.. ¿en que parte me he perdido? 😛
Jaja, que desconfianza tengo en el pobre Herón de Alejandria: Nada mas verlo me pongo a comprobar el caso del triangulo equivalente a la linea a ver si la superficie da 0. Se cumple, se cumple! 😀 Aunque no se de que les debían servir a los sabios antiguos éstas fórmulas, porque para construir partenones no las veo muy útiles. Yo creo que los edificios los construían a ojo, malo sería que se cayeran teniendo tales columnas de piedra, hacían el dibujito de las piezas y el montaje como en los juguetes de los huevos kinder y ya. 😀
Para columnas brutas las de los templos egipcios. Mira las de Karnak por ejemplo, prácticamente no queda espacio entre las columnas. http://www.kirikou.com/egipto/karnak/karnak23.jpg
Las columnas griegas fueron toda una revolución para la época. El material (marmol) y la técnica (el dintel) no daban para más.
¿Y cuál es la demostración de que esto es así? A mí siempre me gusta razonar las fórmulas…..¿Alguien me ayuda?
Cuando usamos la formula típica de (Base)*(Altura)/2, podemos tomar como base y como altura las longitudes de 2 lados cualesquiera. Es mucho mas simple y rápido que la formula de Herón
Sigue el vínculo Fórmula de Herón y lo encuentras,
La fórmula de Heron se usa muchísimo en resolución de problemas.
Para calcular el area de un triangulo (como curiosidad) también se puede hacer a partir del circumradio y el inradio:
A=abc/4R=sr ; siendo s el semiperímetro
Nacho, aunque puedas pensar que construir un partenón es algo facil estas muy equivocado. Esta claro que no es especialmente audaz desde un punto de vista meramente estructural, pero los griegos poseian un manejo de la geometría y de las proporciones envidiable. Por ejemplo, el frente del partenon forma un rectangulo de proporción aúrea, considerada la más armónica, y presente en elementos tanto del mundo vegetal como de nuestro mundo moderno(es la misma proporcion que se observa en las tarjetas de credito). Todas las medidas estaban establecidas en función de una proporcion, lo que se llama el orden, en este caso el diametro en la parte inferior de la columna. Todas las demas medidas se sacaban en función de esta. Por otra parte te sorprendería saber hasta que punto estaban avanzados en terminos constructivos, por ejemplo, la plataforma sobre la cual se asentaba el templo no era totalmente plana, sino que tenia la forma de una porción de esfera, para evacuar las aguas de una manera eficiente y elegante….
En resumén.. aunque a simple vista puedan parecer construciones simples o sencillas tienen mucho trabajo detras que es necesario conocer para poder evaluarlas en su justa medida.
Mi primera respuesta al leer el titulo iba a ser la de seno o coseno para hallar la altura… Desconocia esta formula de herón..
Nevermind: La prueba y los detalles
y los detalles  .
.
Remo, el link «los detalles» no funciona.
Muchas gracias. (Como ves, mis comentarios vuelven a ser los de siempre ;D)
Es porque se le ha olvidado la ‘h’ de ‘href’. El link es el siguiente: los detalles .
Arreglado lo uno, y no dudaba de lo otro. Gracias, Nevermind 😉
[Mode_Matemático_Listillo=On]
Existe otra razón para no usar esa fórmula aparte de que es un tocho infumable (aunque suficientemente simétrico como para ser recordado).
Los griegos no habían desarrollado la notación que usamos actualmente y la gran mayoría de sus razonamientos eran puramente geométricos (del tipo que hoy llamamos Geometría Sintética). Es decir, sin coordenadas ni sistemas de referencia.
Así pues para un matemático griego tenía sentido sumar varias longitudes para encontrar otra longitud y multiplicar dos o tres longitudes para encontrar un área o un volumen pero no cuatro (por mucho que la raiz cuadrada las divida por dos).
En ese sentido es una fórmula que siempre dió bastante mal rollo en la antigua Grecia y que se usó muy poquito a la hora de demostrar otros teoremas, quedando así olvidada. A pesar de ello cualquier Matemático de hoy en día la conoce y gran parte de los alumnos de Bachillerato científico/tecnológico deberían haberla visto alguna vez.
[Mode_Matemático_Listillo=Off]
En la notación de mi libro de Matemáticas viene de forma más sencilla.
S=sqrt[p·(p-a)·(p-b)·(p-c)]
Dónde:
S:=superficie
p:=semiperímetro (perímetro partido por dos)
a, b, c:=lados del triángulo.
Viene a ser el mismo, pero más fácil de recordar.
Felicidades por vuestro excelente blog.
Con respecto a la fórmula de Herón, hay algunos aspectos que puede resultar interesante añadir:
1. La demostración original de Herón es mucho más enrevesada que la expuesta (al menos para nuestro gusto actual). Hay que tener en cuenta que eran demostraciones geométricas, basadas en proporciones y conservación de ángulos, no en transformaciones algebraicas. Se puede ver completa en el recomendable libro de William Dunham «Viaje a través de los genios».
2. Existen dudas razonables de que la fórmula se deba efectivamente a Herón (esto es muy frecuente en matemáticas, tanto, que a menudo basta conocer el nombre propio asociado al teorema para saber quien no fue el primero en descubrirlo). En un antiguo manuscrito, Abu-Rayhan Biruni atribuye el mérito al nunca suficientemente admirado Arquímedes.
3. Hoy existen herramientas muy potentes de cálculo (trigonometría, cálculo vectorial, etc.), pero la simpleza de la fórmula (y sí, para mí es simplísima, comparada con senos y cosenos…) le otorga el tipo de belleza que tanto admiramos los matemáticos.
De nuevo, felicidades, Remo, tienes el don de la claridad (algo que por desgracia cada vez abunda menos). Sigue así, que somos muchos los que te admiramos.
Yo hago 4º de ESO y hicimos esta fórmula hace poco, la trae el libro.
trae la misma fórmula que dice David mh
Curioso, nunca me había planteado que se podía calcular de otra manera que el archiconocido b*h/2. 😀
Lo bueno es que a un griego hace 2000 años sí que se le ocurrió jejeje. Me encanta aprender cosas como esta aunque no sea la forma más práctica de calcular (excepto para algún caso).
Pues yo la fórmula de Herón me ha sacado de más de un apuro. Por ejemplo, para medir la superficie de una parcela cuando solamente tienes una cinta métrica (ni estaciones totales ni nada) es muy útil. Te lías a medir triángulos sin preocuparte de que sean triángulos rectángulos y luego aplicas Herón.
A ver si alguien puede medir la parcela de otra forma (me encantaría descubrirlo). 😉
Libertonia: estoy de acuerdo, aunque existen otros métodos:
Si tenemos un triángulo, pongamos, de lados 5, 5 y 6 (tomemos este lado como base), podemos aplicar el «teorema del coseno» para hallar el coseno de uno de los ángulos interiores. Así podemos obtener, en el ejemplo, que el coseno del ángulo opuesto al lado 5 vale 3/5. De aquí se deduce que el seno vale 4/5.
Ahora bien, por la definición de seno, 4/5 es la proporción entre la altura que queremos hallar y el lado de valor 5. Así que la altura vale 4. Como la base es 6, el área vale 12 u.c.
Pero resulta evidente que hace rato que hubiéramos acabado todo el cálculo si hubiésemos empleado la fórmula de Herón.
Efectivamente , me parece una expresion muy bella . Tiene una especie de simetria…
También se puede calcular como el módulo del producto vectorial de los dos vectores que forman el triángulo.
Pues yo, estudiante de 2º de bachillerato que empecé comentando la fórmula no la había visto jamás cosa aún más extraña contando que mis dos padres son profesores de matemáticas y ésta debiera ser mi asignatura predilecta 😀 Pero bueno, de hecho en las olimpiadas de matemáticas de este año se me tropezó un problema de un triangulo circunscrito en el que pedían demostrar no se que relación, aún así quedé clasificado, la universidad me dió un puñetero puzzle de 100 piezas de regalo, que féliz soy!!!!! jajaja. Un amigo quedó clasificado para la fase nacional de la olimpiada de física, matemáticas y química, las tres. Le diré que ponga algún post a ver si es tan deslumbrante! 😀
Y por cierto a cuenta de lo que me dijo trufas me acorde de que en la película de El pato Donald en pais de las matemáticas venía lo del rectángulo aúreo y su aplicación en esculturas, el Partenón …. He encontrado el frágmento de la regla de oro de la peli en youtube, aquí os pongo el enlace, está en portugues pero se entiende y os invito a que la veais (me encanta la pelicula, como un enano me lo paso :D):
http://www.youtube.com/watch?v=SUSyRUkFKHY&mode=related&search=
Y otros dos que tambien he encontrado 😀 ya de paso:
http://www.youtube.com/watch?v=T8PIIk3_qt8&mode=related&search=
http://www.youtube.com/watch?v=7S3iW_sbqsA
Me excuso de antemano, pero le sigo dando vueltas al asunto. Todo lo que sigue no lo he leído ni lo sé de buena tinta, sólo son conjeturas mías basadas en la práctica matemática cotidiana.
Nicolás preguntaba: «¿Por qué es tan poco conocido ese método, si aparentemente es el más útil en la vida real?»
Ya expresé mi opinión de que considero la fórmula útil y bella. No insistiré en esto.
Creo que la expresión de Nicolás «tan poco conocido» ya ha sido aclarada: en realidad, es bastante conocido. Pero detrás de esa pregunta creo que se encuentra esta otra: «¿Por qué es tan poco utilizada?».
Papá Oso ya apuntó una razón histórica, basada en el concepto geométrico que en la Antigua Grecia había de las magnitudes lineales. Pero Alejandría queda algo lejana en el tiempo. ¿Qué hay detrás de esta maravillosa fórmula que frenó su uso durante siglos hasta la actualidad?
Creo que la respuesta está en Descartes. La revolución que supuso en las matemáticas la creación de un sistema de coordenadas, transformó la geometría en una rama del álgebra. La medida de los segmentos pasó a ser distancias entre puntos coordenados. Una consecuencia del cambio del protagonismo fue que las «medidas enteras» perdieron su papel principal para cederlo a las «coordenadas enteras».
Ahora cojamos la servilleta de papel (Remo: ¿cuándo podremos subir imágenes en los comentarios?) y dibujemos los ejes de coordenadas. Dibujemos también un triángulo con vértices en los puntos (0,0), (2,2) y (3,1). En la cuadrícula cartesiana, se ve inmediatamente que el área de este triángulo es la diferencia entre el área de un rectángulo y la suma de áreas de tres triángulos rectángulos. El sencillo y exacto resultado es de 2 unidades cuadradas.
Pero si tratamos de aplicar la fórmula de Herón… ¡pardiez! Las medidas de los lados del triángulo (aplicando el teorema de Pitágoras) no son números enteros: raíz de 8, raíz de 2, raíz de 10. La maravillosa fórmula se convierte en un monstruo, una expresión numérica complicadísima de calcular con precisión, a no ser que usemos herramientas modernas como una calculadora o un ordenador.
En nuestra era de calculadoras y ordenadores, el problema de la facilidad y precisión del cálculo ya no representa tantas limitaciones. Tal vez por ello se nos olvide con frecuencia la importancia que tuvo en las épocas anteriores. Y esto me lleva a pensar que nuestra era de la «coma flotante» puede que fomente un resurgimiento de la fórmula de Herón.
Transformando algebraicamente la fórmula de Herón, podemos llegar a otra fórmula que desde ya podemos bautizar como La fórmula de Arquímedes-Herón-CPI para hallar el área de un triángulo cuyos vértices tengan coordenadas enteras y en general cualesquiera sabidas las longitudes de sus lados:
Área = 1/4 sqrt[ (a^2 + b^2 + c^2)^2 – 2(a^4 + b^4 + c^4) ]
Ejemplo: Si los vértices son (0,0), (2,2) y (3,1), entonces a^2 es 8, b^2 es 2 y c^2 es 10. Aplicando la fórmula anterior, obtenemos rápidamente y con total precisión el área de 2 unidades cuadradas. ¡CPI siempre vence!
Hablando de coordenadas y triángulos: ¿no es una auténtica fórmula CPI la conocida como fórmula de Pick?
Área = B/2 + I -1
donde B = «nº de puntos del Borde»; I = «nº de puntos del Interior» (puntos de la malla cuadriculada, se entiende).
Aplicándola al ejemplo del triángulo anterior, tendríamos (simplemente contando los puntos en la servilleta) que B=4 e I=1, así que el área es 2 unidades cuadradas. (No aconsejo aplicar esta fórmula en triángulos grandes, a no ser que no se tenga otra cosa más inútil en qué perder el tiempo…)
¿Habeis visto el problema de matemáticas que una Universidad China pone a sus alumnos como examen de Selectividad?
Parece que la Real Academia Británica de Química pagará una pasta a quien sea capaz de contestar a la cuestión.
Yo lo he echado un ojo, y la verdad es que ni siquiera sé muy bien qué es lo que se pregunta. Parece un problema que con el teorema del coseno y Pitágoras a tutiplén puede resolverse…
¿Qué os parece??
Me parece raro ante todo, porque sólo debe de ser una rayada con sistemas de deducción básicos(trigonometria, Pitagoras…en plan los de las olimpiadas de mates), no van a poner la superdeducción de cerebrito en una prueba de acceso por muy raros que sean los chinos. Pero a ver, que no me ha quedado claro, el objetivo es: ¿qué llegue un profesor de universidad lo haga y se lleve 740 euros? ¿que llegue un chino, lo haga y se lleve 740 euros? ¿que llegue el pato donald, lo haga y se lleve 740 euros :D(ver mi anterior post)?
Pues yo con tres lados… sucumbiría a trazarlo con AutoCAD y que la compu averigüe el área. Lo cual me lleva a pensar que somo extremadamente device-dependant (Ver el Manifiesto Inconcluso de Bruce Mau). Y que para colomo no sacamos el mayor provecho posible a todas las herrameintas a nuestro alcance (el cerebro incluido en la lista negra)
La formula es verdaderamente interesante, pero la pregunta que hacía Nicolás era si era posible calcular el área a partir de dos lados y en la formula de Herón hemos tenido que utilizar los tres. A pesar de que mis conocimientos matemáticos son escasos, creo que no es posible calcular el área a partir de dos lados sin que nos den ningún dato más, ya que a esos dos lados dados le pueden corresponder infinidad de triángulos y por tanto infinidad de áreas (…o tal vez no??)
Xondo: La pregunta dice claramente «A partir de los lados», no «A partir de dos lados». Para resolver un triángulo, es decir, sacar sus tres lados y sus tres ángulos, necesitas:
a) Los tres lados, o bien
b) Dos lados y un ángulo. O bien,
c) Un lado y dos ángulos
O sea, que sólo con dos lados no lo sacas.
Esta es mi resolución del problema chino de selectividad que se publica en «El País» y que la academia británica de química dice dar 500 libras a quien lo consiga resolver… no comment.
Se observa que ABD es isósceles y comparte el lado BD con BCD,
luego BCD también es isósceles, y
AE=EC
EB=ED
Por pitágoras:
AC=sqrt((AD^2+DC^2)=sqrt(4+12)=4;
Por el teorema del coseno:
AE=(AD^2-DC^2+AC^2)/2AC=(4-12+16)/2*4=8/8=1
EC=4-1=3
Por pitágoras:
ED=sqrt(AD^2-AE^2)=sqrt(4-1)=sqrt(3)
o bien:
ED=sqrt(DC^2-EC^2)=sqrt(12-9)=sqrt(3)
Construimos un sistema de coordenadas centrado en A,
con eje X coincidente con AC (BD es paralelo a Y por ser
perpendicular a AC):
A={0,0,0}
B={1,-sqrt(3),0}
C={4,0,0}
D={1,sqrt(3),0}
E={1,0,0}
A1={0,0,sqrt(3)}
B1={1,-sqrt(3),sqrt(3)}
C1={4,0,sqrt(3)}
D1={1,sqrt(3),sqrt(3)}
BD={1-1,sqrt(3)-(-sqrt(3)),0-0}={0,2sqrt(3),0}
A1C={4-0,0-0,0-sqrt(3)}={-4,0,-sqrt(3)}
BD y A1C son perpendiculares si su producto escalar es 0:
BD*A1C=(0*-4)+(2sqrt(3)*0)+(0*-sqrt(3))=0
Y queda probado el punto (i).
Ya que el plano definido por el triángulo A1EC1 es perpendicular
a los planos EDC y EDD1, basta calcular el ángulo de los vectores
A1E y EC1
A1E={1-0,0-0,0-sqrt(3)}={1,0,-sqrt(3)}
EC1={4-1,0-0,sqrt(3)-0}={3,0,sqrt(3)}
cos a=A1E*EC1/(||A1E||*||EC1||)=
(3-3)/sqrt((1+3)*(9+3))=0/4=0;
acos (a)=90º, los planos son perpendiculares.
Y queda resuelto el punto (ii)
AD={1-0,sqrt(3)-0,0-0}={1,sqrt(3),0}
BC1={4-1,0-(-sqrt(3)),sqrt(3)-0}={3,sqrt(3),sqrt(3)}
AD*BC1=3*1+sqrt(3)*sqrt(3)+sqrt(3)*0=3+3+0=6
||AD||*||BC1||= sqrt(1+3+0)*sqrt(9+3+3)=sqrt(4*15)=sqrt(60)
cos (a)=6/sqrt(60)=0,77459666924148337703585307995648
acos (a)= 39,231520483592256154931314244744º
Y queda resuelto el punto (iii)
¿Dónde están mis 500 libras 🙂 ?
Jeje, después de haber dormido unas horas he repasado el cálculo que hice y me doy cuenta que en (i) la primera coordenada de A1C es 4 y no -4, aunque da lo mismo porque el producto escalar sigue siendo cero.
Y en (ii) no es 0/4 sino 0/sqrt(60) que sigue siendo 0. Las soluciones están bien (por lo que he podido leer en el foro y otras página) pero solo era corregir esos pequeños fallos.
perdón, sqrt(4*12)=sqrt(48) y no sqrt(60) por lo que me autocorrijo en la autocorrección de (ii). Jeje, mi calculadora mental no funciona bien, jajaja.
Resulta curioso la formula puesta asi en principio parece muy complicada, pero y puesta de esta forma.
http://img.photobucket.com/albums/v213/josefpm/heron.jpg
Es mucho mas facil de recordar, solo te acuerda de la raiz de la suma de los lados entre cuatro y que esa suma va multiplicada pro otras suma donde se va restando cada vez uno de los sumandos, esto es (a+b+c)(-a+b+c)(a-b+c)(a+b-c), resulta bastante facil de recordar y si en lugar de letras tenemos el valor de los lados es multiplicar 4 nuemros hacele la raiz y dividir por 4.
Muchisimo mas facil que calcular senos y cosenos.
a mi me la enseñaron en la prepa agropecuaria, recuerdo que nos llevaron a medir una terreno iregular, con un trancito, teniamos que tomar angulos con la brujula, despues en la libreta hacer triangulos y ppor ultimo sacar el area de cada uno para al final sumarlos y asi sacar el area total, segun recuerdo la formula de b*h/2 no se aplica a todos los triangulos
Aun recuerdo, hace tiempo, que mi padre y mi tio compraron una pequeña parcela e hicieron el siguiente razonamiento: conociendo los cuatro lados, todos de distinto tamaño y sabiendo que el area del cuadrado es lado por lado, pues hacemos la media de los cuatro lados y la elevamos al cuadrado.
P.ej. digamos que los lados eran 12, 30, 23 y 50 metros. Hicieron la media (12+30+23+50)/4=28,75
Y lo elevaron al cuadrado = 826,5 m2
El vendedor acepto la tecnica!
Podria ser una aproximacion de Feinnman? 😀
Salieron ganando o perdiendo?
Cual seria el area correcta?
Un saludo
Kalevala,
pensándolo muy rápido creo que sobrestimaron el área, puesto que lo que hicieron fué conservar el perímetro y suponer que era un cuadrado. Creo recordar que el cuadrado es la figura de cuatro lados que más área encierra dado un cierto perímetro. Así que, me parece, los 826.5 m2 serían un área máxima, casi seguro que lo que compraron tenía menos superficie.
Es demasiado tarde para andar pensando en la forma correcta de calcularlo, aunque seguro que alguno de los cerebritos habituales te dará una fórmula exacta. Yo creo que lo haría dividiendo el área en figuras más simples.
Ricardo, b*h/2 es siempre la fórmula para calcular el área de un triángulo, sólo hay que saber elegir b y h correctamente!!!!!
Saludos y buenas noches